Science Academique

More results...

Generic selectors
Exact matches only
Search in title
Search in content
Post Type Selectors
Filter by Categories
Biology
Current issue
Earth Science
Engineering and Technology
Health Science
Latest articles
Life Science
Medical Science
Physical Sciences
Social Science

Dynamic Symmetry in Quantum-Classical Mechanics: Simplicity in Complexity

Vladimir V. Egorov*

Dynamic Symmetry in Quantum-Classical Mechanics: Simplicity in Complexity

Vladimir V. Egorov*

Mar 6, 2022 Physical Sciences Author: Egorov VV, et al. Type of Article: Review Article
Download Pdf

Russian Academy of Sciences, FSRC “Crystallography and Photonics”, Photochemistry Center, Moscow, Russia

*Correspondence to: Vladimir V. Egorov

Citation: Egorov VV (2022) Dynamic Symmetry in Quantum-Classical Mechanics: Simplicity in Complexity. Sci Academique 3(1): 1-11

Received: 08 February, 2022; Accepted: 26 February, 2022; Publication: 02 March, 2022

Abstract

All kinds of dynamic symmetries in quantum-classical (dozy-chaos) mechanics of elementary electron and/or proton transfers, their physical meaning and applications are discussed.

Keywords: Molecular quantum transitions; Singularity; Dozy chaos; Quantum-classical mechanics; Charge transfer; Condensed matter; Direct and reverse processes; Optical band shapes; Egorov resonance

Introduction to quantum-classical mechanics As is well known, elementary transfers of electrons and/or protons in the membranes of living cells are integral parts of their functioning (see, e.g., [1,2] and references therein). Therefore, in particular, fundamental theoretical knowledge about the elementary transfers of electrons and/or protons in condensed media is of great interest.

The theory of elementary transfers of electrons and/or protons in condensed media is based on a new physical theory – quantum-classical mechanics [3-6]. As a new theory, quantum-classical mechanics arose as a result of eliminating the singularity that occurs in quantum mechanics in the rates of elementary electron-charge transfers when going beyond the Born-Oppenheimer adiabatic approximation and the Franсk-Condon principle [7,8]. This singularity can be easily demonstrated by the example of a one-dimensional potential box with a movable wall [9,10] (Figure 1). In quantum-classical mechanics, the singularity is eliminated by replacing the infinitesimal imaginary addition iϒ in the energy denominator of the total Green’s function of the system by a finite value ϒ>0 [6–8]. The energy ϒ can be considered as the width of the electron-vibrational energy levels in the transient state of the “quantum” transition. However, as shown by a successful comparison of the theory with a large number of experimental data on the shape of the optical bands of polymethine dyes and their aggregates, the energy ϒ is much higher than the energy of the vibrational quantum ħω :  ϒ >>ħω [6]. This fact means physically that in the transient state the exchange of motion and energy between the electron (proton) and nuclei is so intense that it leads to chaos both in the motion of the electron and in the motion of nuclei. This chaos is called dozy chaos, and the corresponding new theory is called dozy-chaos mechanics [6]. Dozy chaos leads to the continuity of the energy spectrum in the transient state of the system, which is characteristic of classical mechanics. While the initial and final states of the system can be considered as quantum states in the adiabatic approximation, which differ sharply in their electron-nuclear structure. Therefore, dozy-chaos mechanics can also be called quantum-classical mechanics [6].

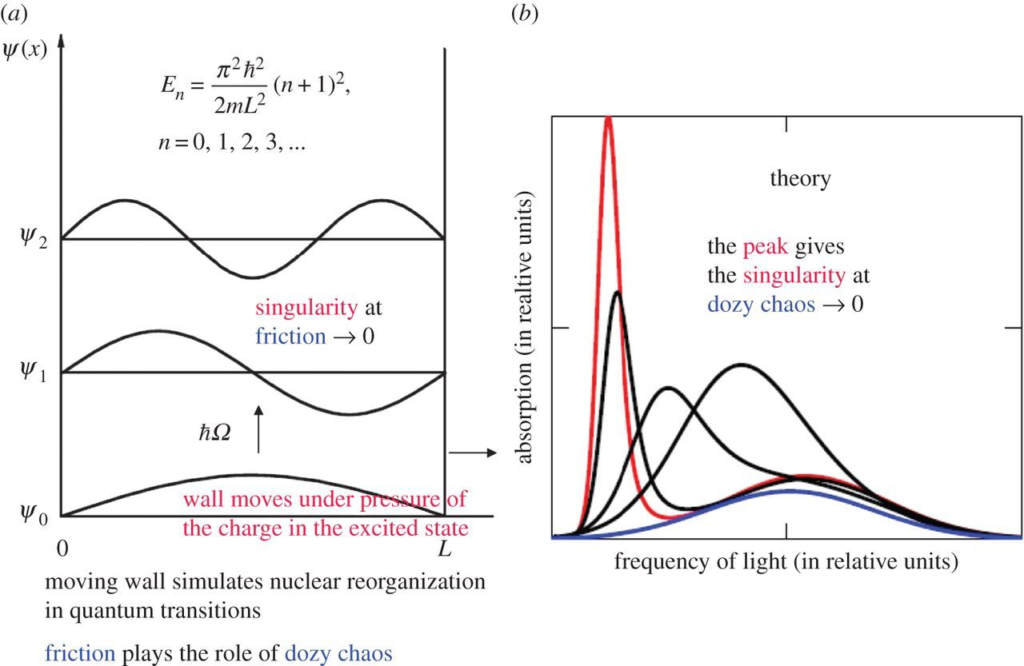
Figure 1: Singularity in the rate of molecular quantum transitions: a potential box with a movable wall (a) and the optical absorption band shape dependent on the dozy chaos available to a given quantum transition (b); the band shape with the strongly pronounced peak (J-band) corresponds to the least dozy chaos [9]. The wall is fastened to the abscissa axis by a freely movable hinge and can move with a certain friction or without friction against the axis. Such a wall simulates the environmental nuclear reorganization in the molecular “quantum” transitions, where dozy chaos plays the role of friction. In the theory [6], this results in the dozy-chaos dependent optical absorption band being displaced to the red spectral region and narrowed (b). The position, the intensity and the width of the optical absorption band are determined by the ratio between the dozy-chaos energy ϒ and the reorganization energy E (see Section 2). The smaller the value of ϒ is, the higher the degree of organization of the molecular “quantum” transition, and the more the intensity and less the width of the optical band (b). The position of the wing maximum is determined by the energy Ε, whereas the position of the peak is determined by the energy ϒ [9]. At high energies ϒ, the band shape is close to symmetric and is Gaussian-like. With a decrease in the value of ϒ, in the red region of the spectrum, a peak appears against the background of a Gaussian-like band, which, with decreasing ϒ, shifts more and more to the red region of the spectrum and becomes more and more pronounced. Thus, with a decrease in the value of the dozy-chaos energy ϒ, the band shape transforms from symmetric to asymmetric [4]. (Original citation)—reproduced by permission of The Royal Society of Chemistry.

Elementary electron transfer, Egorov resonance, and associated symmetries The simplest version of quantum-classical mechanics is the quantum-classical mechanics of elementary electron transfer in condensed media [6]. One of the remarkable features of this theory is the presence of the so-called Egorov resonance – a resonance between the motion of an electron between a donor and an acceptor and the accompanying motion of reorganization of the environmental nuclei [3-12]:

where Ʈe is the characteristic time of motion of the electron in the donor-acceptor system, and Ʈ is the characteristic time of motion of the reorganization of nuclear vibrations in the environment. These times are given by the following equations

where L is the distance between the donor 1 and the acceptor 2 of an electron ( L is equal to the length of the polymethine chain — the main optical chromophore of polymethine dyes) [7-10,12], J1 is the binding energy of the electron on the donor 1 (electronic energy of the ground state of the dye) [7–10,12], m is the effective mass of the electron, and

where E is the energy of reorganization of the nuclear vibrations in the medium.
The Egorov resonance explains the fundamental experimental data on the resonant nature of the change in the shape of the optical absorption band and its intensity in the Brooker series [13] of a polymethine dye, in which the length of the polymethine chain is varied (Figure 2).
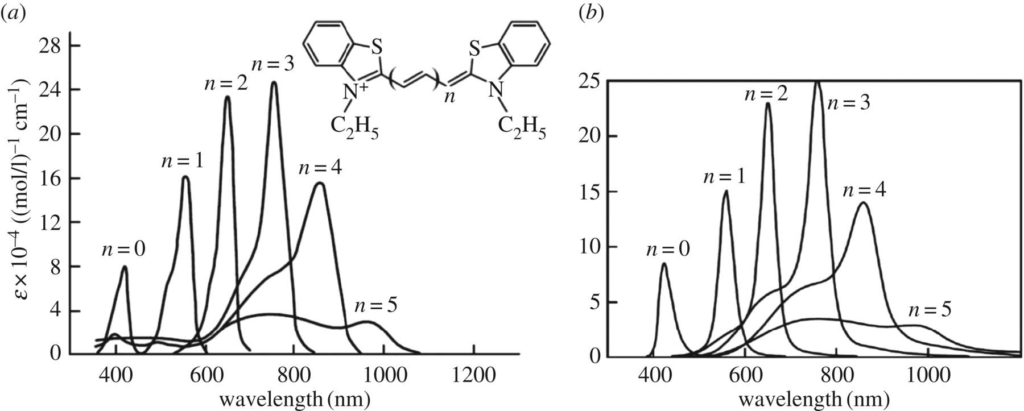
Figure 2: Experimental [13] (a) and theoretical [8] (b) monomer’s optical absorption spectra dependent on the length of the polymethine chain L = 2(n + 2)d, where d are certain roughly equal bond lengths (0.14 nm) in the chain (thiapolymethinecyanine in methanol at room temperature; ε is the extinction coefficient) [9,10]. The optical absorption band with n = 3 corresponds to the dynamic electron–nuclear–reorganization resonance (the Egorov resonance) or is close to it. (Original citation)—reproduced by permission of The Royal Society of Chemistry

The presence of symmetry in the shape of optical bands at high (room) temperatures and large ϒ (Figure 1b) is associated with a primitive, Franck–Condon picture of the dynamics of molecular “quantum” transitions. The loss of this symmetry and the appearance of a peak against the background of a wide band wing are related to the effect of self-organization of transition dynamics in dozy-chaos mechanics, which is expressed, in particular, in the “pumping” of dozy chaos from one part of the optical band to another part (from the peak to the wing, see Figure 1b). In a similar context, the series for the shape of the optical bands of a representative polymethine dye, thiapolymethinecyanine, depending on the length of its polymethine chain L, has a quasi-symmetric character with respect to the Egorov resonance (Figure 2), which corresponds to the most organized quantum-classical transition. Note that the Egorov resonance (Er) is a bright nano-phenomenon, since, for example, for the Brooker series (Figure 2), this resonance is near L­ (Er) = 2 (3 + 2) 0.14 nm = 1.4 nm.

The result for the optical transition-rate constant in quantum-classical mechanics does not change when the sign of the dozy-chaos energy ϒ is changed. This symmetry with respect to the change in the sign of ϒ is consistent with the physical case that both the virtual acts of transformation of electron movements and energies into nuclear reorganization movements and energies and the reverse acts occur in the transient dozy-chaos state [9,10]. For definiteness, we set ϒ > 0 here, there, and everywhere. The Egorov resonance also explains the nature of the well-known narrow and intense J-band of J-aggregates of polymethine dyes [6-8,14-16], which have many different applications (see [16] and references therein).

The Egorov Resonance and Its “Antisymmetric Twin”

The five principal parameters of the problem, viz. electron mass m, electron-donor binding energy J1 = J, distance between the donor and the acceptor L, environmental reorganization energy E, and dozy-chaos energy γ, may be combined into three quantities:

having a time dimension and representing two physically meaningful resonances [8,16]:
The former resonance is between the extended electron motion and the ordered constituent of the environmental nuclear reorganization motion, i.e., it is the Egorov resonance (cf. Equations (1)–(3)). The latter is between the electron motion and, conversely, the chaotic constituent of nuclear reorganization. Since the dozy-chaos energy γ can be considered in a sense as the imaginary part of a complex reorganization energy in which the reorganization energy E is its real part [9], then this second resonance can be considered as some antisymmetric twin with respect to the Egorov resonance. These both resonances can be regarded as the simplest dynamic invariants for the transient state. These dynamic resonance-invariants are alternative to the Born–Oppenheimer adiabatic invariants (potential energy surfaces). In other words, these two resonances are the simplest manifestation of the relationship between electron and nuclear movements in the transient state.
 
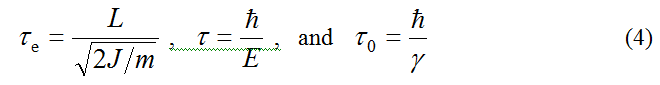
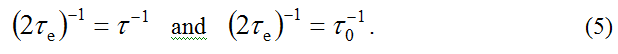
Details of the transient-state-dynamics interpretation based on the Heisenberg uncertainty relation can be found in [8,16]. In particular, according to this interpretation, in the simplest cases, elementary electron transfers can be considered as a motion of a free electron-phonon quasiparticle, the so-called transferon, corresponding to the Egorov resonance, or alternatively, as a motion of a free electron-phonon antiquasiparticle, the so-called dissipon, corresponding to the antisymmetric twin of the Egorov resonance.
 
Symmetry between optical absorption and luminescence in the standard theory [17] and its violation in quantum-classical mechanics as a consequence of the dynamic organization of quantum-classical transitions, which being observed in experiment, is discussed in [4,12].

A Simplified Version of Quantum-Classical Mechanics. Nonradiative Transitions

The results of quantum-classical mechanics for the optical spectra of polymethine dyes, discussed above, and their J-aggregates [6-8,16] refer, in particular, to cases of sufficiently high self-organization of quantum-classical transitions, which correspond, generally speaking, to weak dozy chaos (γ ≤ E or  γ << E). Cases of low self-organization of quantum-classical transitions, corresponding to strong dozy chaos (γ ≥ E), can be interpreted theoretically on the basis of some simplified version of quantum-classical mechanics. The theoretical construction of this simplified version is based on the fact that under strong dozy chaos, the rates of quantum-classical transitions weakly depend on the details of the chaotic dynamics of the transient state [6,10]. These rates depend mainly on the quantum structure of the initial and final states. In other words, the case of strong dozy chaos corresponds to a slight deviation of quantum-classical mechanics from the standard theory based on the Born-Oppenheimer adiabatic approximation and the Franck-Condon principle.In this case, one can avoid considering the dependence of the complete Green’s function of the system on the finite imaginary addition iγ, and the Green’s function of elementary electron-charge transfers in condensed media can be approximated by the Gamow exponent depending on the transient energy ħω1 of the phonon environment (see [6] and references therein).Physically, this circumstance allows us to speak about the nature of the transient state not in terms of dozy chaos, but in terms of a large number of tunnel and over-barrier transitions promoting the “quantum” transition of an elementary charged particle. This theory [18] was developed long before the creation of quantum-classical mechanics, and now it can be considered as its simplified version.On the basis of this simplified version of quantum-classical mechanics, explanations were given for the Brӧnsted laws in proton-transfer reactions [19-21] (see Section 5) and the temperature-dependent electron transfers in Langmuir-Blodgett films (see Refs 20,46 in [6]). From the general result for the rate constant in the simplified version of quantum-classical mechanics [18], in the framework of the Einstein model of nuclear vibrations (ωk = constant = ω) the simple expression for the rate constant K has been obtained [18]:

The result (6) applies to both optical and nonradiative processes. In the case of optical processes, the heat energy ħω12 is determined from the law of conservation of energy
(ħω12>0 – absorption and ħω12<0 – luminescence), where the frequency Ω=0 in the cases of nonradiative endothermic and exothermic processes:
In the case of the complete theory for optical processes [6,12], the expression for the rate constant of the reverse process Krev is obtained by changing the sign in the heat energy ħω12 and in the donor-acceptor distance L in corresponding expression for the rate constant of the direct process K [12]. In the considered simplified version of quantum-classical mechanics, applying this position to Equation (6), we obtain
Where Keq exp(- 4L/a) is the equilibrium constant of charged-particle-transfer reactions in the simplified version of quantum-classical mechanics. In the limit L→0, we obtain from Equation (11) the well-known detailed balance relationship in statistical physics and in the standard theory of many-phonon transitions [17].
 
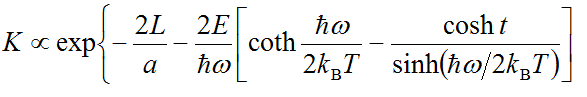
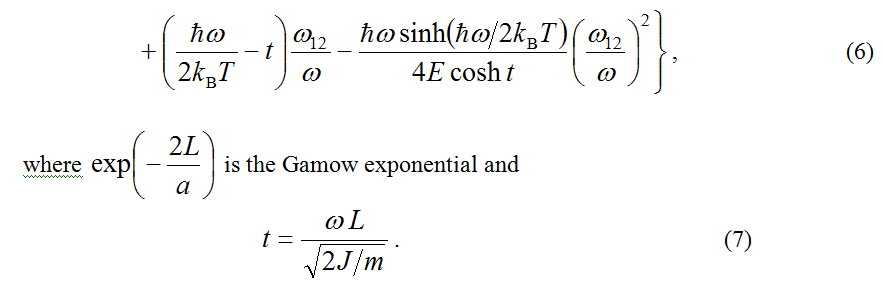
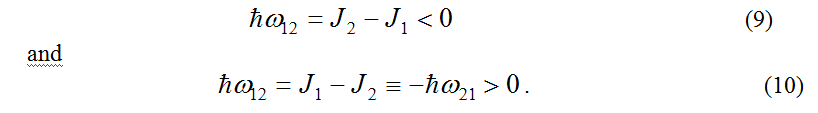
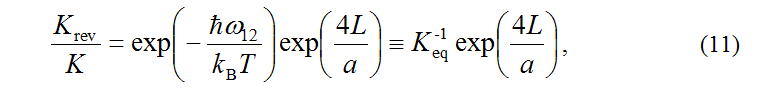
The Simplified Version of Quantum-Classical Mechanics: Proton-Transfer Reactions. On Symmetry in the Brӧnsted relationships
 
Grounded on the simplified version of quantum-classical mechanics [18], the author [19] gave a theoretical explanation of the main experimental regularities in proton-transfer reactions, or in other words, in acid-base catalysis, which were established by Brӧnsted back in the twenties of the last century [20].The simplified version of quantum-classical mechanics is directly related to elementary electron transfers. To extend it to elementary proton-transfer reactions, it is necessary to take into account thermal fluctuations in the width of the electronic potential barrier (donor-acceptor distance L).Due to the large size of the wave function of an electron when it is localized on a donor and/or on an acceptor, the electron transfer rates, in contrast to the proton transfer rates, are not sensitive to thermal fluctuations in the barrier width. An analytical formula for the proton-transfer rate constant is obtained within the simplified version of quantum-classical mechanics. The Brӧnsted relationships for acid and base catalysis are
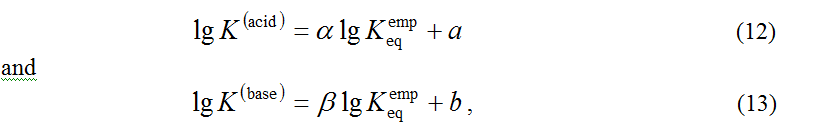
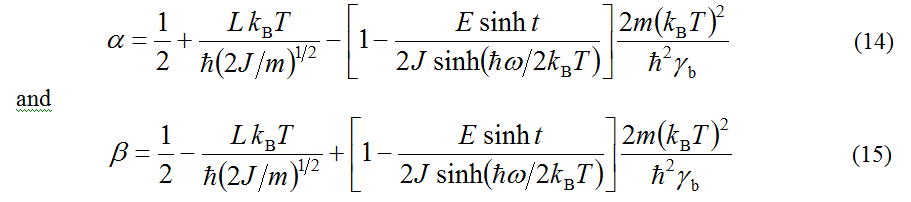
where K(acid) and K(base) are the rate constants, Keqemp is the empirical equilibrium constant, and α , β and a,b are constants. The Brönsted coefficients α and β obtained from the simplified version of quantum-classical mechanics (the Einstein model of nuclear vibrations (ωk = constant = ω) for direct (acid catalysis) and inverse (base catalysis) reactions [19]
(t is given by Equation (7) and γb is barrier rigidity) are symmetric relative to 1/2 and meet the generally known empirical equality [21]

(which directly follows from the Brӧnsted relationships (12) and (13)).

The Simplified Version of Quantum-Classical Mechanics: Symmetrization of the Amplitude and Rate Constant of the Transition for the Case of Different Electron-Phonon Interactions on the Donor and Acceptor

Until now, both in the case of the complete theory for optical processes (Sections 1–3) and in the case of its simplified version for nonradiative processes (Sections 4,5), we have considered the case of the same electron-phonon interaction when a light charged particle, in particular an electron, is localized on the donor or on the acceptor. In other words, it was assumed that the reorganization energy E=E1=E2. For example, “quantum” transitions and the corresponding shapes of optical bands in polymethine dyes are well described by the case of the same value of the electron-phonon interaction on the donor and on the acceptor, because charge alternation occurs in the polymethine chain upon optical excitation [5,10,12]. In this section, we will briefly consider the case of different electron-phonon interactions when an electron is localized on a donor 1 or acceptor 2. This corresponds to different in magnitude the reorganization energy E1≠E2. For example, in the case of nonradiative processes, the change in sign in the heat energy ħω12 (Equations (9) and (10)) and in the donor-acceptor distance L=|L=L12| is associated with the permutation of indices 1 and 2 in the reverse order. The assumption E1 ≠ E2 leads to asymmetry with respect to the permutation of indices 1 and 2 in the expression for the rate constant of transitions and the loss of connection between forward and reverse processes, expressed in Equation (11). To restore this connection, it is necessary to symmetrize the expression for the amplitude and rate constant of electron transfers with respect to different values of the electron-phonon interaction at the donor and at the acceptor, which leads to the case of reorganization energies E1 ≠ E2. The symmetrization method proposed in [22] consists in the fact that, in addition to the transition amplitude [6,10,12]

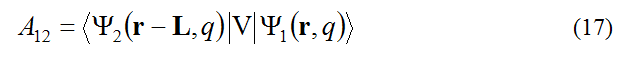
(r and q are electron and phonon coordinates) which, in view of taking the wave function Ψ2 in the Born-Oppenheimer adiabatic approximation Ψ2 = Ψ2BO  and taking into account the entire dynamics of the transition only in the wave function Ψ1, can be called the amplitude of the transition on the acceptor A12a, we introduce into the theory also the amplitude

in which, on the contrary, the wave function Ψ1 is taken in the adiabatic approximation Ψ1 = Ψ1BO, and the entire dynamics of the transition is taken into account only in the wave function Ψ2. This new amplitude A12d can be called the amplitude of the transition on the donor. Then the half-sum of these two amplitudes is taken as the total transition amplitude:
Since the symmetrization is carried out only with respect to the electron-phonon interaction, in Equation (19) the permutation of indices 1 and 2 in the quantity L12 is not performed and the sign of
Using Equation (19), for the case of different electron-phonon interactions on the donor and acceptor in the framework of the Einstein model of nuclear vibrations (ωk = constant = ω) the simple analytical expression for the rate constant has been obtained [22]:
where e±t = exp(±t). Substituting E2 = E1 = E into Equation (20), we obtain Equation (6) for the rate constant in the case of the same electron-phonon interaction on the donor and acceptor. It is easy to see that Equation (20) satisfies the relationship of detailed balance in the simplified version of quantum-classical mechanics (Equation (11)).
 
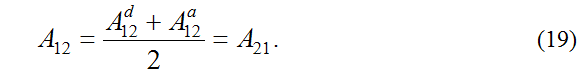
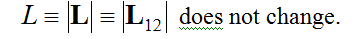
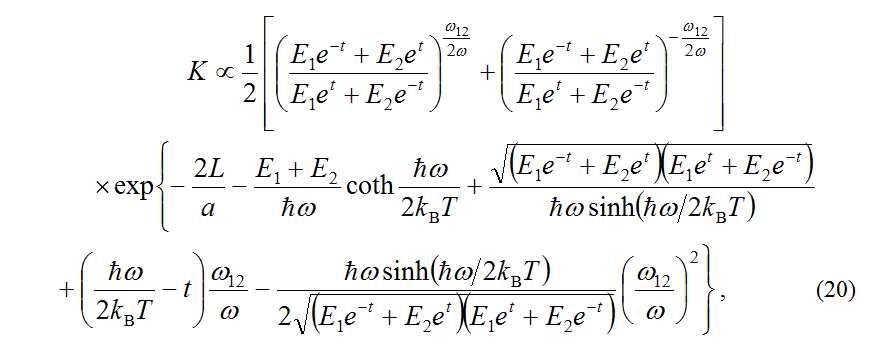
Conclusions
 
It is of interest to generalize quantum-classical (dozy-chaos) mechanics for optical processes in its full formulation (Sections 1–3) to the case of different electron–phonon interactions on the donor and acceptor (Section 6), as well as to construct a theory of nonradiative dozy-chaos processes (Sections 4,5) in its full version. An important point in the formulation of the problem in the theory of nonradiative dozy-chaos processes is the determination of the perturbation operator in the amplitude of transitions which causes the nonradiative transitions. It is also of interest to generalize quantum-classical mechanics to the case of nonlinear optics [3-5,11].
 
Funding: This work was supported by the Ministry of Science and Higher Education within the State assignment Federal Scientific Research Center “Crystallography and Photonics” Russian Academy of Sciences.

References

  1. Teixeira LR, Cordas CM, Fonseca MP, Duke NEC, Pokkuluri PR, et al. (2020) Modulation of the Redox Potential and Electron/Proton Transfer Mechanisms in the Outer Membrane Cytochrome OmcF From Geobacter sulfurreducens. Front Microbiol 10: 2941.
  2. Björck ML, Brzezinski P (2018) Control of transmembrane charge transfer in cytochrome c oxidase by the membrane potential. Nat Commun 9: 3187.
  3. Egorov VV, Thomas S (2021) Quantum–classical mechanics: On the problem of a two-photon resonance band shape in polymethine dyes. Nano-Structures & Nano-Objects 25: 100650.
  4. Egorov VV (2020) Dynamic Symmetry in Dozy-Chaos Mechanics. Symmetry 12: 1856.
  5. Egorov VV (2020) Dozy-Chaos Mechanics for a Broad Audience. Challenges 11: 16.
  6. Egorov VV (2019) Quantum-classical mechanics as an alternative to quantum mechanics in molecular and chemical physics. Heliyon 5: e02579.
  7. Egorov VV (2001) On electrodynamics of extended multiphonon transitions and nature of the J-band. Chem Phys 269: 251-283.
  8. Egorov VV (2002) Nature of the optical transition in polymethine dyes and J-aggregates. J Chem Phys 116: 3090.
  9. Egorov VV (2013) Optical lineshapes for dimers of polymethine dyes: dozy-chaos theory of quantum transitions and Frenkel exciton effect. RSC Adv 3: 4598.
  10. Egorov VV (2017) Nature of the optical band shapes in polymethine dyes and H-aggregates: dozy chaos and excitons. Comparison with dimers, H*- and J-aggregates. Royal Soc Open Sci 4: 160550.
  11. Petrenko A, Stein M (2019) Toward a Molecular Reorganization Energy-Based Analysis of Third-Order Nonlinear Optical Properties of Polymethine Dyes and J-Aggregates. J Phys Chem A 123: 9321.
  12. Egorov VV (2019) Quantum-classical mechanics: Luminescence spectra in polymethine dyes and J-aggregates. Nature of the small Stokes shift. Res Phys 13: 102252.
  13. Brooker LGS, Sprague RH, Smyth CP, Lewis GL (1940) Color and Constitution. I. Halochromism of Anhydronium Bases Related to the Cyanine Dyes1. J Am Chem Soc 62: 1116-1125.
  14. Jelley EE (1936) Spectral Absorption and Fluorescence of Dyes in the Molecular State. Nature (London) 138: 1009-1010.
  15. Scheibe G (1936) Variability of the Absorption Spectra of Some Sensitizing Dyes and Its Cause. Angew Chem 49: 563.
  16. Egorov VV (2009) Theory of the J-band: From the Frenkel exciton to charge transfer. Phys Procedia 2: 223-326.
  17. Perlin YE (1964) Modern methods in the theory of many-phonon processes. Sov Phys Usp 6: 542-565.
  18. Egorov VV (1988) Theory of tunnel transfer, Khim. Fiz 7: 1466-1482 [Sov. J. Chem. Phys., 1991, 7: 2629-2660].
  19. Egorov VV (1990) Effects of fluctuations in the transparency of the barrier in proton transfer reactions. Russ J Phys Chem 64: 1245.
  20. Brönsted JN (1928) Acid and Basic Catalysis. Chem Rev 5: 231-338.
  21. Bell RP (1959) The Proton in Chemistry; Cornell University Press: Ithaca, New York.
  22. Egorov VV (1994) Towards theory of elementary charge transfers in acid-base catalysis. Russ J Phys Chem 68: 221.
Visit Us On FacebookVisit Us On Linkedin