Quantum fluids and superfluidity

Navin Khaneja^*

System and Control Engineering, IIT Bombay, Powai, India

*Correspondence to: Navin Khaneja

Citation: Khaneja N (2024) Quantum fluids and superfluidity. Sci Academique 6(1): 01-15.

Received: 10 December, 2024; Accepted: 11 January, 2025; Published:18 January, 2025

Abstract

In this paper, we study viscosity, and superfluidity. Water molecules are hydrogen bonded, to form a collection, a basic fluid element, we call corpuscle. The corpuscles have relative veloc- ity among themselves, and ineleastically scatter to cut down relative velocity. They exchange momentum, and change of center of mass energy goes into exciting phonons (vibrations) in a corpuscle, and we heat the corpuscle. This is viscosity. The corpuscles interaction is small, compared to thermal energy and we treat them as free. When we cool water at 0^◦, the corpuscle becomes very ordered, and phase change happens and all water dipoles get oriented. Then all corpuscles talk very strongly, and we have a solid. In liquid helium, the dipole interact weakly and we can make it very cold, before it becomes solid and before solid forms the corpuscle undergoes a Bose Einstein condensation, where the corpuscle which is now collection of atomic waves, have all of them in ground state, with a big energy difference to next excited state. This means the corpuscle cannot inelastically scatter, as excitation energy is too high, and we have superfluidity. Our main contribution in this paper is, we are more explicit and elaborate, where literature is terse and succinct.

Corpuscle

The water dipole has a moment of inertia of I ∼ 10⁻⁴⁶ and thus have a rotational microwave resonance at

but experience with microwave ovens tells that this resonance is much lower ω ∼ 10⁹, signifying I is much larger, we have a collection of water molecules, a corpuscle. What is typical I

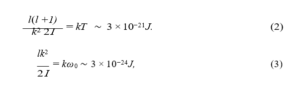
ω₀ = 3Ghz. Then l = 10³. Then I = 10⁻⁴²Kgm²,

moment of inertial

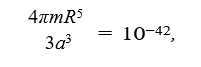
R = 3 × 10⁻⁹, approx N = 10³ molecules make a corpuscle.

 Figure 1: Shows an atom collection, corpuscle.

Two dipoles at distance R have coulomb attraction energy  e²/4ΠQ₀R  ( d/R)², which for R ∼ A^◦

is 1eV for (d/R)² ∼ 1/10.

Two corpuscles 100A^◦ away, have a coulomb attraction energy of 10 meV, with dipole ordering parameter θ ∼ 10⁻², which is comparable to thermal energy k_BT ∼ 30meV at room temperature.

Phase Transitions

When temperature is lowered, dipoles in corpuscle become ordered, it is a Ising Model and at critical point, they are all ordered and θ shoots up, locking all corpuscles into a solid [1].

 Viscosity and ineleastic scattering

Let’s calculate the viscosity, two corpuscles scatter travelling at velocity v + u and v − u scatter exchange photon and go to velocities v and v , the change of momentum is ^dmu _dt= muχ = µ( ^u R²). The scattering amplitude is

For kk = mu, and approx u to be 1 m/s, variation over cm or 10⁻⁶m/s over Corpuscular   dimension, which gives k ∼ 10⁵ or Rk ∼ 10⁻³. This gives µ ∼ 10⁻³Pascal − s. This is the viscosity of water

Vibration modes of Corpuscle and orbitals

Corpuscle is just a lattice with phonon like vibrational modes. The wave-vector of the the modes is in the Brillouin zone of dimension ^2π/a with a spacing between modes of ^2π/R . The dispersion relation is ω = υk where υ is velocity of sound in the medium. When dipoles r apart are stretched by ∆r, the energy increases ^k∆r2/2 with k, the spring constant k, this gives

K=e²/4Πq₀r²Δr(d/r)². With ∆r ∼ A^◦, we get k ∼ 1 N/m and we get υ ∼ 1000 m/s.

Take helium, which doesn’t solidify, as we cool the corpuscle, individual atoms have debroglie wavelength comparable to corpuscle dimension, then we have to talk about atomic orbitals of the corpuscle, in a central potential which is the dipolar potential of other atomic waves, which is just R² potential as shell model in nuclear physics. Except in dipolar potential, we have factor of (d/R)², which makes it a square well potential and its orbitals are as shown in Fig. 2.

Scrub and Scatter

Two corpuscles scatter travelling at velocity v + u and v − u scatter exchange photon and go to velocities v and v, The energy decreases and internal (vibration) modes of the corpuscle are excited, heating the corpuscle. This is shown in Fig. 3.

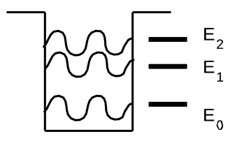
Figure 2: Fig. shows square well potential and its orbitals.

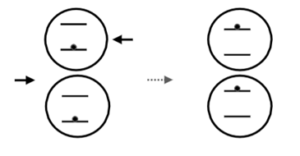
Figure 3: Shows how two corpuscles scatter raising their internal energy.

Bose Condensation and Superfluidity

In liquid helium II, the dipole interact weakly and we can make it very cold before it becomes solid and before solid forms the corpuscle undergoes a Bose Einstein condensation, where the corpuscle which is now collection of atomic waves have all of them in ground state with a big energy difference to next excited state. This means the corpuscle cannot inelastically scatter as excitation energy is too high and we have superfluidity [2, 3]. This is shown in Fig. 4.

Properties of Superfluids

Wall creep

Fig. 5 shows supefluid creep up walls of container and flow out of vessel. Fluid likes the wall due to stronger adhesive forces and can exchange momentum with walls and climb up. It doesn’t happen in a normal fluid as the momentum is dissipated in the fluid, which is not true in superfluid.

Fountain

Fig. 6 shows how radiation differentially heats the bulb fluid which due to superfluidity is not efficiently dissipated into the outer fluid and we see a fountain.

Vortex

Fig. 7 shows quantized vortices in rotating vessel containing the fluid. The rotating vessel, will transfer angular momentum to fluid till both angular momentum equalize. Then we look for a fluid configuration with minimal energy, which is when we form vortices. Because if L is the total angular momentum and I the inertia of the fluid, we get total energy as ^L . If I form N vortices each carrying ^L , worth of angular momentum then the energy is

L²/LNI. The vortex is just a Bose corpuscle, where one or more atom is in excited state worth carrying nk or angular momentum.

Second sound

When we differentially heat a superfluid, adding kinetic energy in a given direction, the kinetic energy doesn’t move in all direction, as we do not scrub against other corpuscles and we have only movement if kinetic energy or temperature in the given direction at a sound

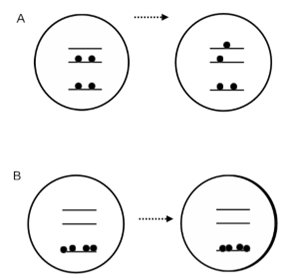
Figure 4: Shows superfluidity arising due to phenomenon of Bose condensation.

Figure 5: Shows superfluid creep up walls of container and flow out of vessel.

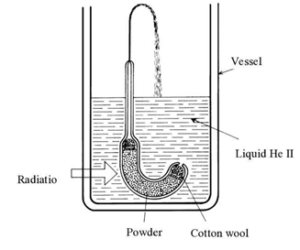
Figure 6: Shows the supefluid Fountain.

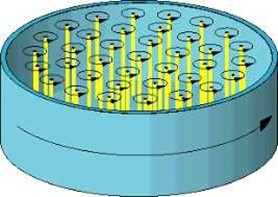
Figure 7: Shows superfluid vortices in rotating vessel containing the fluid.

which is much smaller, then how fast a pressure wave moves which is first sound. This is shown in Fig. 8.

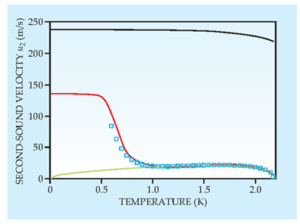
Figure 8: Shows speed of second sound.

Pairing and Supefluidity in Helium III

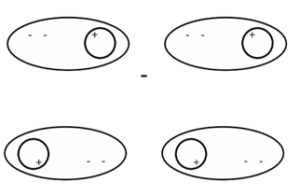
Figure 9: Shows how two He³ atoms pair and form a molecule.

Turbulence

Figure 10 show turbulent flow, where streamlines curve. Fig. shows this arises because the corpuscles scatter at an angle. When relative velocity is too high the scattering amplitude is low (k is high in χ in 4) and corpuscles do not scatter, but if they scatter at an angle then the scattering amplitude rises and scattering takes place. This is turbulence.

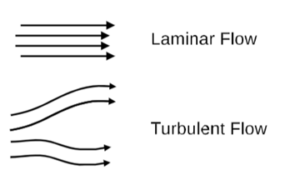
Figure 10: Show turbulent flow arising when corpuscles scatter at an angle.

Water Waves

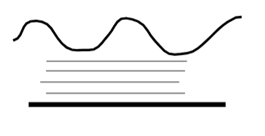
Figure 11: Shows water waves in 2-Dim.

Consider water waves in in two dimensions x − z as in 11, the displacement u along x

direction satisfies,

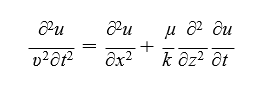
The solution (z measured from top of water) is of the form u(x, z, t) = exp(ik_xx + k_zz −iωt)), which gives,

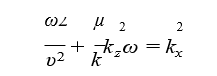
For z negative, near the bed, the velocity dies. The real solution is of course u(x, z, t) = exp(k_zz) cos(kx − ωt)). When the corpuscle, velocity is high on the top at the crest of the waves, the pressure by Bernoulli principle is low and the water rises at the crest to give water waves. This is as shown in 12. The upward force as shown in the 13, arises due to the term (κ = k/R spring constant per units length)

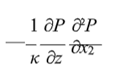
along the z direction where (P is pressure) we have again a wave equation in the z direction. The wave equation in x and z direction are coupled by this term which makes water rise.

Figure 12: Shows water waves where water rises and dips, crests and troughs at the top.

When we accelerate, the fluid with x dependent acceleration it has non-trivial inner product with a mode and hence excites the mode and we get waves as in ocean waves where the centrifugal force due to earth spinning has tangential component which has θ dependence as in fig. 14.

When water wave is driven with a impulse (say excess pressure at the origin) a waves will be excited which will flow out, if different modes are excited which travel outwards with different speed and we get water crests as in 15.

Figure 13: Shows upward thrust due to second derivative of pressure.

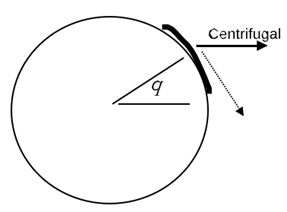
Figure 14: shows when centrifugal force on ocean water is resolved along q direction, it has q dependence which excited the mode.

Figure 15: Shows water riipples when we drop a pebble on water surface.

Conclusion

In this paper, we studied viscosity, and superfluidity. Water molecules are hydrogen bonded, to form a collection, a basic fluid element, we call corpuscle. The corpuscles have relative veloc- ity among themselves, and ineleastically scatter to cut down relative velocity. They exchange momentum, and change of center of mass energy goes into exciting phonons (vibrations) in a corpuscle, and we heat the corpuscle. This is viscosity. The corpuscles interaction is small, compared to thermal energy and we treat them as free. When we cool water at 0^◦, the corpuscle becomes very ordered, and phase change happens and all water dipoles get oriented. Then all corpuscles talk very strongly, and we have a solid. In liquid helium, the dipole interact weakly and we can make it very cold, before it becomes solid and before solid forms the corpuscle undergoes a Bose Einstein condensation, where the corpuscle which is now collection of atomic waves, have all of them in ground state, with a big energy difference to next excited state. This means the corpuscle cannot inelastically scatter, as excitation energy is too high, and we have superfluidity. Our main contribution in this paper was, we were more explicit and elaborate, where literature is terse and succinct. We studied turbulence and superfluidity in Helium III.

References

1. Pathria RK, Statistical Butterworth-Heinemann (1996).
2. Tony Gu´enault, Basic superfluids, Taylor and Francis (2003).
3. Tilley DR, Tilley J, Superfluidity and Superconductivity, Institute of Physics (1996).
4. Lee DM, Osheroff DD, Richardson RC, Reviews of Modern Physics 69: 645-690, (1997).
5. Osheroff DD, Richardson RC, Lee DM, Rev. Letters 28, 885 (1972).
6. Leggett AJ, Mod. Phys. 47, 331 (1975).
7. Vollhardt and P. Wo¨lfle, The Superfluid Phases of Helium -3, Taylor and Francis, London (1990).
8. Volovik GE, Exotic Properties of Superfluid Helium 3, World Scientific (1992)